How Does a Spectrometer Work? Principles Explained

A USB spectrometer is the most common type of spectrometer. They take light, separate it by wavelength and create a spectrum which shows the relative intensity of these separate wavelengths. Spectrometers have a wide range of applications and uses.

Broadly speaking, all optical spectrometers consist of an entrance slit, a diffraction grating or prism, a detector, and routing optics. The entrance slit allows light into the spectrometer, where a system of mirrors or lenses routes it first onto a diffraction grating or prism, and then onto the detector. The grating or prism splits the light into its constituent wavelength components, and the detector records the light intensity as a function of wavelength. If the spectrometer has a large spectral range, it may also have filters to stop higher order light from reaching the sensor. Most optical spectrometers operate over the UV, visible, and infrared (or near-infrared) regions of the electromagnetic spectrum.

Spectrometers can be designed and built using a number of different optical configurations.

Spectrometer Components

---

Entrance Slit

Light enters the optical spectrometer via the entrance slit. Similarly to how the aperture size of a camera affects the brightness and resolution of its photos, the width of the spectrometer entrance slit determines both its ability to measure in low-light conditions and the maximum spectral resolution that you can achieve.

These two characteristics must be balanced against each other as one will always come at the expense of the other. A wide entrance slit allows a lot of light to enter the spectrometer, which allows fainter sources to be measured but reduces the spectral resolution of the system. Conversely, a narrow entrance slit can increase the spectral resolution, but at the cost of signal intensity.

Larger optical spectrometers may have a controllable slit width, while more compact devices like the Ossila USB Spectrometer (which has an entrance slit width of 25 μm) usually have a fixed width.

Diffraction Grating or Prism

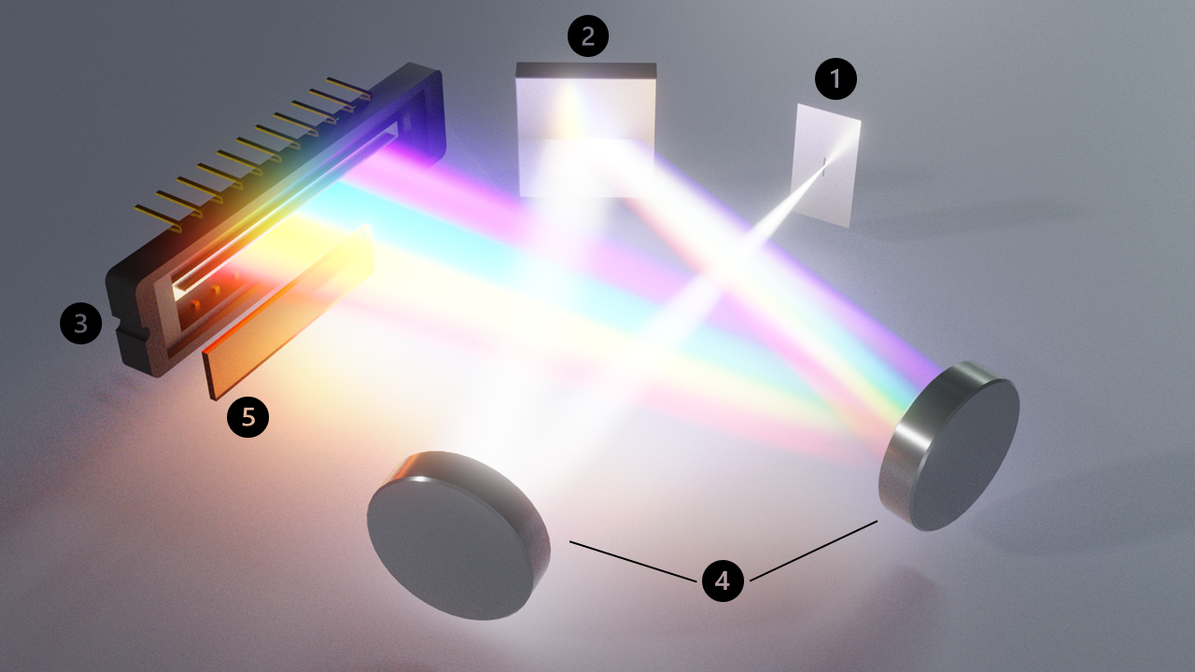
The optical diffraction grating is the component that splits the light into its constituent wavelength components. There are a number of different types of gratings including transmissive, reflective, ruled, and holographic. Each has their own advantages and disadvantages when compared to one another, and there is no one superior design.

The design of the grating determines to what degree the light is spread out. Much like the slit, there is a trade-off between resolution, range, and signal strength.

Diffraction gratings can be described by the equation:

Where d is the grating spacing, θ_m is the diffraction angle of the m^th diffraction order, θ_i is the angle of incidence, and λ is the wavelength of the light. From this, you can see that decreasing the grating spacing will increase the angular range of diffraction. Therefore, a smaller range of wavelengths will reach the detector with reduced signal strength, but with higher resolution. Conversely, increasing the grating spacing gives a bigger range of wavelengths but with lower resolution.

The grating spacing is usually quoted in terms of groove density, which is equal to 1/d and is given in units of grooves mm^-1.

In some spectrometers, the diffraction grating can be rotated to allow different wavelengths to hit the detector. Here, the acquisition window will be selected according to need. Similarly, some spectrometers have multiple gratings with different groove densities, which can be selected between.

Some designs of optical spectrometer use a prism as the dispersive element in place of a diffraction grating, but due to the higher cost of prisms and the lower resolution images that they give, this is not common.

Detector

The optical detector records the intensity of the light that reaches it as a function of its wavelength. Spectrometer detectors consist of a row of light sensitive pixels, each of which corresponds to a particular wavelength. Each pixel will generate an electrical signal of intensity proportional to how much light falls on it.

Charged-coupled devices (CCDs) are the detector of choice for spectrometers due to their high dynamic range and uniform pixel response. To reduce unwanted noise in the spectra, CCDs are usually cooled to combat dark current signals.

Routing Optics

Internal routing optics direct the light from the entrance slit onto the diffraction grating or prism, and then onto the detector.

Curved mirrors are generally preferred over lenses as they introduce fewer image aberrations. There are many possible configurations for the optics (e.g., Fastie-Ebert, Czerny-Turner) which each have relative advantages and disadvantages regarding optical aberrations, stray light, and size.

Higher Order Filters

If the wavelength detection range of an optical spectrometer spans more than one diffraction order, a filter may be necessary to partially cover the detector and block higher order light from reaching the sensor.

USB Spectrometer

Browse now

Learn More

---