Exciton: An Introduction

Excitons are quasi-particles made up of bound electron and hole pairs. Having a clear understanding of exciton theory is essential in order to understand semiconductor behavior. Exitonic behavior can be examined using various spectroscopy techniques, including a USB spectrometer. Excitonic properties will often determine the potential application of a material in optoelectronic devices, for example as photovoltaics, light-emitting diodes or even as lasers.
When an electron is excited into a higher energy state, either through absorption of a photon or another excitation method (such as in electroluminescence), this creates a positively charged space in the lower energy level known as a “hole.” This results in the formation of an electron-hole pair. In some cases, these two particles exist in a bound state, forming a single quasi-particle known as an exciton. Within an exciton, the electron and hole are bound together by Coulombic interactions, and the strength of this bond is quantified by its exciton binding energy.
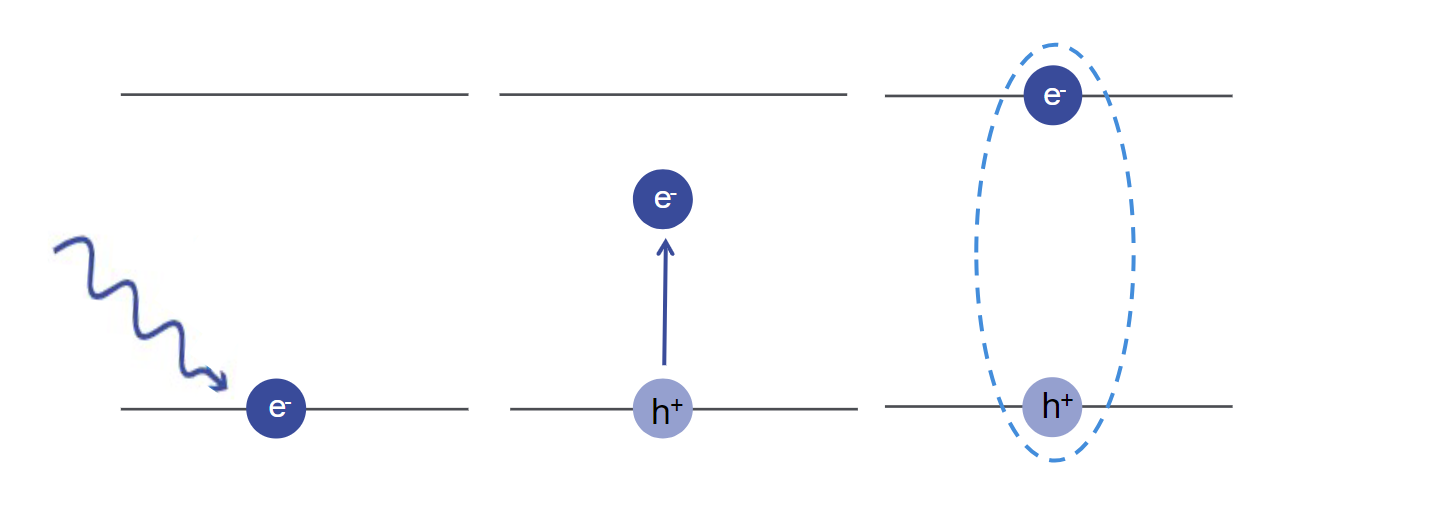
Exciton Binding Energy
Exciton binding energy represents the energy required to dissociate an exciton into its constituent electron and hole charge carriers. A higher exciton binding energy indicates a more stable exciton with a longer lifetime. A materials binding energy is influenced by factors such as the material's dielectric constant, the effective mass of the electron and hole, and the spatial confinement of excitons in quantum dots or nanowires. In most semiconductors, the Coulombic interaction is screened by the other electrons in the valence band, so the exciton binding energy is relatively low. In these cases, you can calculate the exciton binding energy theoretically.
To estimate the exciton binding energy of a material, you can use the following equation:
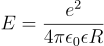
Where e is elementary charge, ε is the dielectric constant of your material, ε0 is the vacuum dielectric constant and R represents the average distance between an electron and hole. However, this method provides a general approximation and may not be suitable for estimating certain exciton binding energies, such as those of organic semiconductors.
In a 3D configuration, such as in a bulk semiconductor crystal, the Rydberg energy of Wannier-Mott excitons (excitons with large radius and high quantum number n) can be predicted using the following equation:
Where μ is the reduced electron mass, m0 is electron mass, Ry is the Rydberg constant, εr is the relative permittivity of your material and n is quantum number. The radius of the exciton (the distance between the electron and hole) can be calculated using the exciton Bohr energy formula:
Where aH is the Bohr radius. You can also measure exciton binding energy experimentally. When carriers in an exciton recombine, the emitted photon's energy will be lower the energy gap between these two energy states (this is often the band gap, EG). The exciton binding energy is equal to the difference between EG and the measured photon emission (Ex) using the following rule:
Excitonic properties can be measured using a range of techniques.
- EX can be measured using standard photoluminescence measurements
- You can measure the free-carrier band gap EG using methods such as scanning tunnelling microscopy.
- You can observe exitonic peaks of a sample using excitonic peaks using simple absorbance measurements. These small peaks can be seen around or below the band gap of a material, indicating the presence of excitons.
In some materials, as the number of excitons increases in a material, an excitonic plasma can form. This exitonic plasma acts as a continuum again and the excitonic peaks disappear.
Considerable research has been conducted to accurately calculate the exciton binding energy for various materials used in different applications. Here, we have included a few examples of exciton binding energies for various semiconductor materials.
| Semiconductor | Exciton Binding Energy |
| GaAs | 4.9 meV |
| CdTe | 11 meV |
| ZnO | 29 meV |
| Organic Semiconductors | 0.1 – 1.0 eV |
| Perovskite Semiconductors | 1 – 20 meV |
Types of Excitons
Excitons can be grouped into two categories: Frenkel excitons and Wannier-Mott excitons.
Frenkel excitons are tightly bound excitons which have a radius similar in magnitude to the crystal unit cell or atomic radii. These are often found in insulators or organic semiconductors, as they are often bound to specific atoms or molecules.
Alternatively, Wannier-Mott excitons have a larger excitonic radius. The exciton therefore encompasses many unit cells so can move more freely through the crystal structure. These are commonly found in inorganic semiconductors, and their exitonic bonds can be overcome at room temperature.
Generally, organic matter such as fullerenes and insulators, tend to exhibit Frenkel excitons with a larger binding energy. These are sometimes known as bound electrons. Most inorganic or hybrid semiconductors (such as perovskites) have Wannier-mott excitons and have free excitons that can travel through the crystal structure.
Excitons in Semiconductors
Semiconductor physics revolves around the excitation and recombination of electrons and holes. Processes like fluorescence or electroluminescence primarily involve the recombination of free electrons and hole carriers, rather than excitons. However, when an exciton does recombine, it emits a photon with energy lower than the material's band gap. This energy difference is the energy required to break the excitonic bond. By employing the aforementioned equations, it becomes possible to calculate the energy of the emitted photon accurately.
In the context of solar cells, the efficient separation of electron-hole pairs is critical for the extraction of free charge carriers that contribute to the generation of electrical energy. A higher binding energy makes it more challenging to separate the electron and hole, potentially leading to a lower solar cell efficiency. Most solar cell materials, such as inorganic silicon pv and hybrid organic-inorganic pv like perovskites, tend to form Wannier-Mott excitons with relatively low binding energies. This characteristic means that charge carriers can easily move through the crystal, increasing the performance of these solar cells.
On the other hand, excitons hold a different significance in organic light-emitting diodes (OLEDs). In organic semiconductors, excitons are bound together as Frenkel excitons, acting as tightly bound quasi-particles. This property becomes advantageous in OLED devices, as reliable radiative recombination of excitons generates light. Frenkel excitons, with their larger binding energies, recombine emitting photons necessary for producing vivid and vibrant colors in OLED displays. However, when it comes to using organic semiconductors in solar cells, the high exciton binding energy poses a challenge. To address this, organic photovoltaicsemploy a donor-acceptor configuration with an energy offset between the two materials, enabling efficient charge separation despite the strong excitonic bonds.
It is worth noting that free electrons and holes in semiconductors can exist in various energy states, resulting in the emission of a range of different photons upon radiative recombination. This poses a limitation when attempting to create monochromatic light sources, such as lasers. The control and manipulation of excitonic processes are areas of active research and development to achieve precise control over emitted photons and enhance the performance of semiconductor-based light sources.
In summary, excitons in semiconductors have a profound impact on the optical and electronic properties of these materials. They influence processes such as recombination, light emission, charge separation, and overall device performance in optoelectronic applications. Understanding the unique characteristics and behaviors of excitons allows researchers and engineers to harness their potential and advance the field of semiconductor technology.
USB Spectrometer

Learn More
 Absorbance Measurement
Absorbance Measurement
Absorbance measurements are crucial in many areas of scientific research. In an absorbance measurement, light over a broad wavelength range passes through a sample and a spectrometer measures the light that is transmitted. Using these transmittance measurements, you can calculate the amount of absorbance at different wavelengths. This article describes how to take an absorbance measurement using an optical spectrometer.
Read more... Polymer-Fullerene Bulk Heterojunction Solar Cells
Polymer-Fullerene Bulk Heterojunction Solar Cells
A solar cell is a device that converts light into electricity via the ‘photovoltaic effect’. They are also commonly called ‘photovoltaic cells’ after this phenomenon, and also to differentiate them from solar thermal devices.
Read more...References
- K. Galkowski et al., “Determination of the exciton binding energy and effective masses for methylammonium and formamidinium lead tri-halide perovskite semiconductors,” (2016) Energy & Environmental Science vol. 9, no. 3, pp. 962–970. doi:10.1039/c5ee03435c
- T. Palmieri et al., “Mahan excitons in room-temperature methylammonium lead bromide perovskites,” (2020) Nature Communications, vol. 11, no. 1. doi:10.1038/s41467-020-14683-5
- Y. Zhu et al., “Exciton binding energy of non‐fullerene electron acceptors,” (2022) Advanced Energy and Sustainability Research, vol. 3, no. 4, p. 2100184. doi:10.1002/aesr.202100184