Radiative Efficiency Limit: The SQ Limit Explained

The radiative efficiency limit (also known as the Shockley-Queisser limit or the detailed balance limit) is the fundamental efficiency limit on single p-n junction solar cells. It was initially named after William Shockley and Hans Queisser, who defined it in 1961 .

Theoretically, the maximum possible efficiency for a single-junction solar cell is 33.7% with an optimum band gap of 1.34 eV. This limit depends on the solar cell bandgap and is calculated considering the fundamental loss mechanisms of a solar cell including thermal losses, spectral losses, radiative recombination losses and parasitic resistance losses.

There are other loss mechanisms that limit the efficiency of solar cells including non-radiative recombination, incomplete absorption, light reflections and contact resistance. However, they are not included (assumed to be zero) in the radiative limit calculations. It primarily assumes the non-radiative recombination as zero - this is why the radiative efficiency limit is named so. Hence, single-junction solar cells can not realistically attain the radiative efficiency limit and can't exceed it. Understanding this fundamental limit and the reasons behind it is essential for photovoltaics research.

Radiative Efficiency Limit: The Theoretical Solar Cell Limit

---

PCE of a single-junction solar cell device is given as:

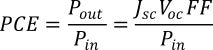
Here V_OC is the open-circuit voltage, J_SC is the short-circuit current, FF is the fill factor of the device, and P_in is the incident solar power (standard AM1.5G, 100 mW/cm²).

The V_OC is directly proportional to the bandgap of the material (E_g). On the other hand, J_SC declines exponentially as E_g increases. FF also increases with E_g. This consequently leads the maximum theoretical efficiency to follow a trend as given in the figure below.

The fundamental limit on the efficiency of solar cells is given by the maximum theoretical efficiency vs the E_g curve. Each solar cell will have a fundamental efficiency limit depending on its band gap. The maximum efficiency limit for single-junction solar cells is about ~33.7% at E_g ~1.34 eV (also called the optimum bandgap value for solar cells). The SQ limit values for single-junction solar cells have been documented in tabular form by Rühle et al.

Radiative Efficiency Limit: Fundamental Losses

---

Loss mechanisms in solar cells define their fundamental efficiency limit. Understanding these loss mechanisms is essential to improve the solar cell efficiency. There are broadly four fundamental loss mechanisms considered for calculating the radiative efficiency (AKA the Shockley-Queisser) limit as listed below:

1. Thermal Radiation Losses:

Thermal losses occur due to the emission of thermal radiation by the cell itself. Solar cells act as blackbody absorbers, radiating heat energy as a function of its temperature, and will decrease the achievable efficiency. As cell temperature rises, thermal radiation increases.

2. Spectral Losses:

Spectral losses arise from the mismatch between the solar (input) spectrum and the absorption properties of the solar cell material. These losses account for about half of the efficiency loss in a solar cell. These are categorized into two:

• Transmission Losses: Photons with energy < E_g are not absorbed (but are transmitted) by the cell and hence not converted to electricity. Transmission increases as bandgap increases.
• Thermalization Losses: Photons with energy > E_g excite the charge carriers. The excited charge carriers with excess energy cool down to the conduction and valence band edges. The excess energy is released as heat (via lattice vibrations or phonons) and this is known as thermalization. Thermalization increases as bandgap decreases.

3. Radiative Recombination Losses:

Excited charge carriers (electrons and holes) can recombine before they are extracted to an external circuit. This recombination results in an efficiency loss, as the electrons and holes cannot contribute to the current.

In radiative recombination, electrons fall back into the valence band to recombine with the hole. It is called radiative recombination as a photon with the energy equal to the bandgap is radiated in this process. It is also called band-to-band (B2B) recombination. It is a predominant mechanism in direct bandgap semiconductors.

4. Parasitic Resistance Losses:

In the equivalent circuit model of solar cells, there are series and shunt resistances. Series resistances (R_s) account for losses at the junctions (interfaces) and internal losses (e.g. metal-semiconductor junction losses). Shunt resistances (R_sh) account for the leakage currents and bypass paths (e.g. pinholes, device shorting). For better efficiencies, you should aim to minimize R_s and maximize R_sh.

Additional Losses Beyond the Radiative Efficiency Limit

---

There are a few additional losses that result in reduced solar cell efficiency. However, these are not considered (assumed to be zero) in the radiative efficiency limit (AKA Shockley-Queisser limit) calculations:

1. Non-radiative Recombination: While radiative recombination releases a photon, non-radiative recombination happens without radiating a photon. Non-radiative losses can be minimized by preparing better quality (defect-free) devices. There are two types of non-radiative recombination:
• Trap-assisted Recombination: Recombination happens through defect states within the bandgap. This is also called Shockley-Read-Hall (SRH) recombination. This trap-assisted recombination also occurs at the interfaces and is called surface recombination. This recombination is a predominant mechanism in indirect bandgap semiconductors.
• Auger Recombination: Recombination where the energy is transferred to another carrier rather than being emitted as a photon. This recombination is rare and only significant for semiconductors with high charge carrier concentrations (heavy doping).
2. Incomplete absorption: Incomplete absorption in solar cells refers to the phenomenon where not all incident photons are absorbed by the active layer of the solar cell. This can lead to reduced efficiency because fewer electron-hole pairs are generated, resulting in lower current output. However, this loss can be minimized by thickness optimisation and light trapping strategies.
3. Reflection losses: A portion of incident light is reflected off the surface of the solar cell before it can be absorbed. Anti-reflective coatings are often applied to reduce surface reflection and enhance absorption.
4. Contact losses: Contact losses in solar cells refer to the inefficiencies that arise due to the electrical contacts, which are essential for extracting the generated current. This can be minimized by selecting metals with better conductivity as contacts.

Assumptions of Radiative Efficiency Limit

---

The radiative efficiency limit (also known as the Shockley-Queisser limit) for single-junction solar cells is calculated based on some major assumptions:

• It assumes perfect absorption of photons above the bandgap energy and perfect transmission of photons below the bandgap energy.
• The limit is derived using principles of thermodynamics and detailed balance, considering the equilibrium between the absorption of sunlight and the emission of radiation.
• It considers the radiative recombination mechanism only. Non-radiative recombination is not considered.
• It assumes no reflection losses and contact losses.

These assumptions make the radiative efficiency limit value a theoretical benchmark (an upper bound). However, realistically, it is impossible to reach the exact values of the radiative efficiency limit.

Realistically, at standard conditions, non-radiative recombination, incomplete absorption, reflection losses, and contact losses would exist anyway. The better-quality devices with innovative strategies would minimize such losses but to a practical extent. For example, silicon (bandgap ~ 1.12 eV) can theoretically attain 33% efficiency; and even after four-five decades of silicon solar cell research, the maximum efficiency recorded to date is 26.7%.

Overcoming the Radiative Efficiency Limit: Advanced Concepts

---

There are a few advanced concepts in research which you can use to potentially overcome the SQ limit:

Multijunction Solar Cells: One key to overcome the SQ limit is by stacking multiple solar cells. Each cell is optimized to absorb a specific range of the solar spectrum. This enables them to absorb and convert a wider range of solar spectra than single-junction cells. By this way, this innovative design overcomes the single-junction SQ limit. These solar cells stand as the most proven technology in terms of research and commercialization.

Other concepts are still in the research stage and await to be commercially viable.

1. Hot Carrier Solar Cells: Hot carrier solar cells aim to capture and utilize high-energy carriers (electrons and holes) before they lose energy to heat, reducing thermalization losses and improving efficiency.
2. Intermediate Band Solar Cells: Intermediate band solar cells introduce an additional energy band within the semiconductor's bandgap, allowing the absorption of lower-energy photons and enhancing the cell's ability to convert a broader range of the solar spectrum into electricity.
3. Multiple Excitation Generation: Multiple exciton generation involves generating multiple electron-hole pairs (excitons) from a single high-energy photon, thereby increasing the photocurrent and improving the solar cell's efficiency.
4. Upconversion and Downconversion: Upconversion converts low-energy (infrared) photons into higher-energy (visible) photons, while downconversion splits high-energy photons into multiple lower-energy photons. Both aim to better shift the photon towards the solar cells bandgap, so it can be better absorbed and improve efficiency..
5. Plasmonic Solar Cells: Plasmonic solar cells use metal nanoparticles to enhance light absorption through plasmonic resonance, which concentrates light at the nanoscale, improving the efficiency of the solar cell by increasing the local electromagnetic field.
6. Multi-Absorber Solar Cells: Multi-absorber solar cells use multiple materials or layers with different bandgaps to absorb different portions of the solar spectrum. These are similar to tandem cells but are not necessarily stacked vertically. They can be arranged in other configurations to to optimize light capture and efficiency.

Learn More

---

Further Reading

---

Detailed balance limit of efficiency of p-n junction solar cells, Shockley, W., & Queisser, H. J., Journal of Applied Physics (1961)

The Physics of Solar Cells, Nelson J., J. (2003)

View more references