Surface Energy: Formula & Definition

Surface free energy is a measure of the excess energy present at the surface of a material, in comparison to at its bulk. It can be used to describe wetting and adhesion between materials, but is not often used quantitatively. This article will explain the fundamental definition of surface energy, how to calculate it directly using contact angles, and how to tune it to fit your needs. For further information on contact angles, see Ossila's guides to the background theory of contact angle measurements, and how to take them using the Ossila Contact Angle Goniometer.

What is Surface Energy?

---

In the bulk form of a material, atoms are generally stable and have a balanced set of bonds/interactions. In contrast, the surface atoms will have an incomplete, unbalanced set of interactions, and therefore have unrealised bonding energy. Surface energy is a relative measurement of the energy at the surface (which is a result of this incomplete bonding). It is positively correlated to the strength of bulk interactions and the level of surface exposure. Therefore, surface energy will be higher if the bulk interactions are stronger, or if the surface exposure is greater.

A surface will always try and minimise its energy. This can be done by adsorbing a material with a lower energy onto its surface. Through the adsorption process, the number of exposed surface atoms with high surface energy are minimised and replaced with lower energy atoms or molecules. Liquids will often have lower surface energies than solids (due to the weak forces interacting between molecules), which is why liquids usually spread out. Surface energy can be defined as the energy required per unit area to increase the size of the surface, and as such is often quoted in units of mN/m.

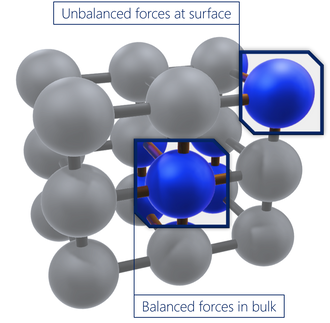
Surface energy is mostly used to describe a solid. The tendency of a solution to spread out (or 'wet') on a solid surface depends on several factors. Here it is assumed that the liquid and solid are capable of similar polarity interactions.

Generally, a surface with a low surface energy will cause poor wetting, and therefore result in a high contact angle. This is because the surface is not capable of forming strong bonds, so there is little energetic reward for the liquid to break bulk bonding in favour of interacting with the surface. Typical surfaces with low surface energy include hydrocarbons, as these are held together with weak Van der Waals forces. A high surface tension liquid will also cause this, as it is more favourable for the solution to maintain bonds with itself.

The opposite is true for a high surface energy, which will generally cause good wetting and a low contact angle. Examples of surfaces with high surface energy include glasses, ceramics, metals, and materials held together by stronger bonds (e.g. ionic, covalent and metallic). A low surface tension liquid will also give a low contact angle- as interactions within the liquid are not that strong.

How can Surface Energy be Calculated?

---

Surface energy is usually measured indirectly with contact angle measurements, which can be a useful qualitative measure. Quantitative data can also be obtained by using a variety of different models. Most of these are based on Young's equation,¹ a form of which is seen in Equation 1:

In the above equation, σ_s is the surface energy of the solid, σ_sl is the interfacial tension between liquid and solid, σ_l is the surface tension of the liquid, and θ is the contact angle of the liquid on the solid.

Dupré's equation can be used to relate interfacial tension and the interactions between the solid and liquid. Interactions are generally described by the work of adhesion, W_sl, which represents the work which must be done to separate the two phases, or the energy released in wetting. This is seen in Equation 2:

This relationship is similar to (but not exactly the same as) that between the interfacial tension and the spreading coefficient, S:

The spreading coefficient measures the tendency for a liquid to wet on a solid, where wetting occurs for positive values.

Equation 2 and Equation 3 can be combined into the Young-Dupré equation, which is the basic form used by many of the surface energy models:

Different models will include different interactions in their calculation of surface energy, meaning values, even for the same sample, are not always directly comparable between them.

Zisman Model

One of the most basic and widely used methods of calculating surface energy is the Zisman model, published in 1964.² This model assumes that the surface energy of a solid is equal to the maximum surface tension liquid that will give a contact angle of 0°. This is known as the critical surface tension.

Contact angle on the surface (in the form cosθ) for a series of liquids is plotted against surface tension. This is then extrapolated to find the surface tension for cosθ = 1, where θ = 0°, and surface tension is equal to the surface energy of the solid.

As the Zisman model ignores the impact of polar interactions, it is only accurate for non-polar surfaces (such as polyethylene). For polar surfaces (including those that contain heteroatoms), a model that includes polar interactions must be used.

Fowkes & Extended Fowkes Model

The most common method of calculating surface energy for polar surfaces is the Fowkes model, published in 1964.³ Fowkes' theory assesses the interactions between a liquid and solid in terms of 'dispersive' (Van der Waals) and 'polar' interactions. These interactions will sum to form overall energy:

Where σ_s^D and σ_s^P are the dispersive and polar components of the surface energy of the solid respectively.

Initial Fowkes theory is shown in Equation 6:

Where σ_l ^D and σ_l ^P are the dispersive and polar components of the surface tension of the liquid respectively. This theory uses the geometric mean for each type of interaction, in contrast to the similar Wu model,⁴ which uses the harmonic mean.

By combining Equation 4 and Equation 6, we can obtain Fowkes' primary equation, seen in Equation 7:

The first step for this surface energy calculation is to measure the contact angle for a purely dispersive liquid, meaning σ_l ^P = 0 and σ_l = σ_l ^D, reducing Equation 7 to Equation 8:

Using this, σ_s^D can be calculated directly, when the surface tension for the liquid is known. A common material used here is diiodomethane, which has effectively no polar component to its surface tension (due to molecular symmetry), meaning σ_l = σ_l ^D = 50.8 mN/m.⁵

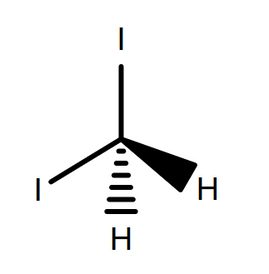
The next step is to measure the contact angle for a liquid with known dispersive and polar components. A common material used here is water, where σ_l ^P = 51.0 mN/m and σ_l ^D = 21.80 mN/m.⁵ By inserting this into Equation 7, along with surface tension and previously calculated σ_s^D, the value of σ_s^P can be calculated. The final surface energy value is then a sum of the surface energy components, as seen in Equation 5.

This model is best for low-charge surfaces that are moderately polar, such as polymers featuring heteroatoms.

Fowkes' model can also be extended⁶ to include a third interaction component, σ^H, which describes the hydrogen bonding within the phase. This calculation therefore requires three liquids with known components, and thus is not used as often as the standard Fowkes model.

Owens-Wendt-Rabel & Kaelble Model

The Owens-Wendt-Rabel & Kaelble model (OWRK) was published in 1969⁷ and 1970.⁸ It is mathematically equivalent to the Fowkes model, but derived from different principles.

The OWRK model is shown in Equation 9:

OWRK requires at least two liquids with known dispersive and polar interactions. If these are not known they can be determined with a reference solid (such as untreated PTFE). This can be assumed⁹ to have a surface energy of ~18.0 mN/m and be incapable of polar interactions, meaning σ_s = σ_s^D = 18 and σ_s^P = 0. By inserting this into Equation 9, we can achieve Equation 10:

As a result, a contact angle on PTFE can be used to calculate σ_l ^D for any liquid where the overall surface tension is known. σ_l ^P can then be calculated using the difference between the overall surface tension and σ_l ^D.

Once dispersive and polar interactions of the liquids are known, they can be used to calculate surface energy of a new surface, by plotting each liquid on a graph in the form of Equation 9. The slope between the points of the liquids will equate to √σ_s^P, and the intercept will equate to √σ_s^D. The overall surface energy can then be calculated using Equation 5.

OWRK can be used for similar materials to Fowkes, but fits better to slightly lower energy surfaces, and requires much more experimental work.

Van Oss-Good Model

Whilst dispersive and polar interactions represent many surfaces well, other significant interactions (such as hydrogen bonds) are not considered by either Fowkes or OWRK. The Van Oss-Good model was published in 1992¹⁰ and considers acid-base interactions. This model combines polar and dispersive interactions into one term, alongside acid (σ ⁺) and base (σ ^-) components. The acid component describes the ability of a surface to interact with a basic liquid (i.e. one that can donate electron density) through polar interactions, such as dipole-dipole bonding and hydrogen bonding. The base component describes the opposite of this (e.g. interactions with an electron-accepting, acidic liquid).

The primary equation for the Oss-Good model can be seen in Equation 11:

By choosing a liquid with only a dispersive component, such as cyclohexane, the equation reduces to Equation 12:

This means the contact angle can be used to calculate σ_s^D. Repeating this with a liquid with no acid component, such as tetrahydrofuran, gives Equation 13:

This can be used to calculate σ_s⁺. Repeating this with a liquid with no base component (e.g. chloroform), will give σ_s^-, which can be used to calculate σ_s by summing all three components. Alternatively, once σ_s^D and either σ_s⁺ or σ_s^- is known, the remaining component can be calculated from Equation 11 by using a liquid with known acid and base components (e.g. water). This is useful if a liquid with no acid/base component is difficult to find.

The Oss-Good model works best for polar surfaces, such as organometallics. However, it can be difficult to establish an unknown acid and base components for liquids because there is no defined set of reference solids.

Which Model Should I Use?

• Non-polar surfaces with low surface energies: Zisman
• Moderately polar surfaces: Fowkes (better for slightly higher energies) or OWRK
• Polar surfaces (inorganic, organometallic and ionic): Oss-Good
• To find polar and dispersive interactions of liquids: Reference surface & Fowkes/OWRK

There are also additional surface energy models that are not discussed here, such as:

• The Wu model:⁴ Good for materials with low surface energy up to 40 mN/m
• The Schultz model:¹¹ Used for high energy surfaces like bare metals
• The Neumann equation of state:¹² Approximates surface energy with only a single liquid by ignoring the impact of different interaction components

How can Surface Energy be changed?

---

A high surface energy is important for solution wetting, especially in processes such as spin coating. Most solids with high surface energy will not maintain a high-energy surface when exposed to atmospheric conditions. Hydrocarbon contaminants present within the air will adsorb onto the solid's surface, reducing the surface energy. The most common method of tuning surface energy is through surface treatment, which is typically designed to raise the energy by removing these contaminants or forming high surface energy functional groups. Many of these techniques only produce temporary changes to the surface energy. This is because adsorption of low surface energy molecules will occur over time slowly reducing the average surface energy.

UV Ozone Treatment

An in-depth description of UV Ozone can be seen on Ossila's UV Ozone Cleaner page. UV radiation will ionise atmospheric oxygen to form oxygen radicals, which will go on to react and form ozone. Radiation of a different wavelength will hit organic molecules, exciting them or forming free radicals, which will allow reaction with the ozone. This forms volatile molecules which can easily desorb from the surface, leaving it clean from contaminants, and with an increased surface energy.

Plasma & Corona Treatment

Plasma treatment is also commonly used to clean surfaces and increase surface energy. Here a gas or gas mixture is ionised by a high frequency voltage to form a reactive gas plasma. This is a mixture of free radicals, ions, electrons and gas molecules. The plasma will interact with the surface in several ways. Contaminants can be removed via ablation, by bombardment with electrons and ions, or through reactions with species in the plasma. This can form volatile organic molecules that will desorb (and sometimes also replace) contaminants with high surface energy functional groups, such as C=O and HO-. In some cases, plasma treatment can etch the surface and affect surface roughness. The exact impact of plasma treatment will depend on the gas used, for example oxygen plasma will react with and oxidise organic contaminants, whereas argon and other inert gases may only remove contaminants through ablation.

Corona treatment is similar to atmospheric plasma, but uses a lower plasma density. Here, the ionised gas is created by discharging a high frequency voltage across an electrode over a grounded surface. The film is passed underneath the electrode, and the surface is oxidised to remove contaminants and raise surface energy.

Beyond UV ozone and plasma treatment, other common methods of raising surface energy include flame treatment, etching and coating a high surface energy interfacial layer of a different material.

Lowering Surface Energy

In some cases (e.g. to generate a hydrophobic coating), surface energy needs to be lowered instead of increased. This is typically done with a coating of a lower surface energy material (e.g. a wax), or through specific surface microstructures that are designed to minimise solution wetting.¹³

UV Ozone Cleaner

Browse now